THE DOPPLER EFFECT
When we derived the wavelength-frequency relationship,
v = f λ , we
assumed that the observer and source were standing still. Suppose the observer
is fixed and the source is moving towards the observer at a speed
u
and emitting a sound of frequency f
so that the time elapsed between two
successive crests is 1/f.
As shown on the graph below, the distance travelled by the first crest in
this time will be
v/f
.
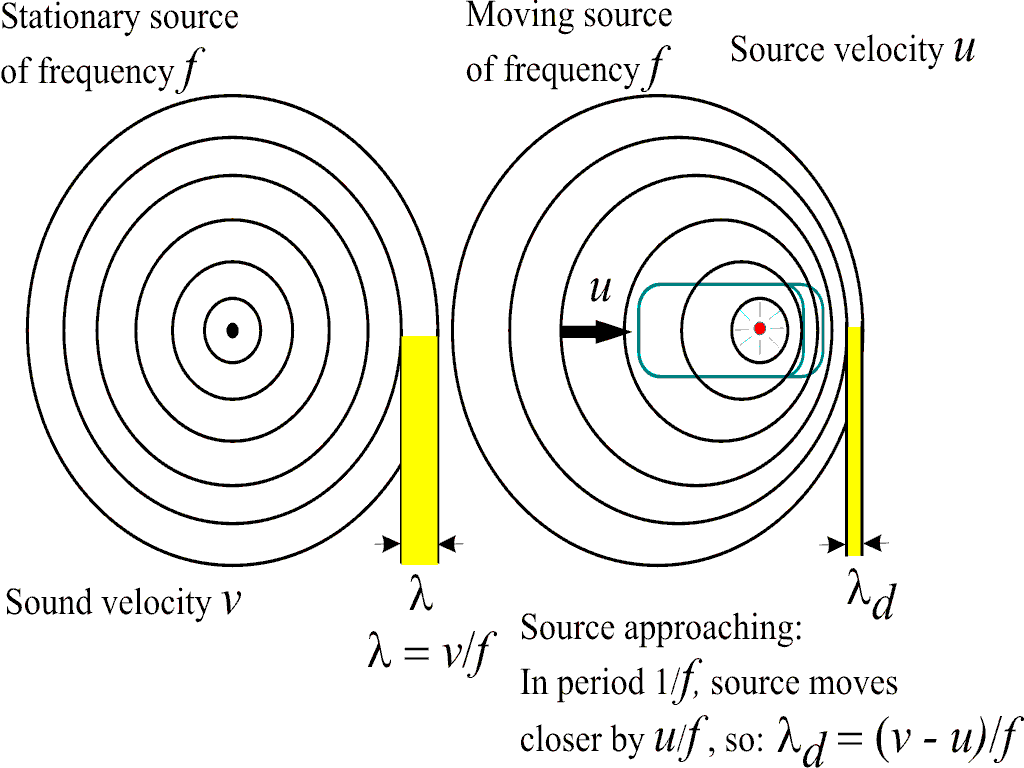
In the meantime, the
source will have travelled a distance
u/f.
Therefore, the distance between crests, also called the wavelength, is
v/f - u/f.
Thus the perceived frequency (fd)
is related to the actual frequency
f of the source and the relative
speed of the source u
by:
fd=fv/(v-u)
This shift in frequency
of waves which results from sources or observers moving with respect to
the medium is called the Doppler effect. It was first explained
by Christian Doppler in 1842. This effect also holds true for light waves.
In this case, a change in frequency is perceived as a
change in colour. An example is given by the red shift of light from remote
galaxies moving away from our galaxy. As for acoustic waves, the Doppler
effect can be observed when listening to the gradual change of pitch in an
ambulance siren as it passes by.
Subsonic source :
u < v
An illustration of
the Doppler effect is given by the animation below. It shows the
successive wavefronts emitted by a source moving at a speed lower than the wavefront speed (or speed of sound). It can be seen that, in front of the
source, the wavefronts start to bunch up whereas they stretch further
apart behind the source. As a result, an observer located in front of the
source will perceive a higher frequency than an observer located behind
the source.

Transonic source
: u = v
If the source moves at
exactly the speed of sound (that is
about 340 m/s in air under room conditions), it can be seen that the wavefronts in
front of the source are now all bunched up at the same point, resulting in
a shock wave. As a result, an observer in front of the source will detect
nothing until the source arrives. The energy in the sound waves cannot get
away from the source, and this is why aeroplanes undergo extreme forces as
they pass through the 'sound barrier'.

Supersonic source
: u > v
If the source is now
travelling faster than the speed of sound, the sound source may pass by a
fixed observer before the observer actually hears the sound it creates.
Then, as the shock wave passes by, the observer will perceive a
"bang"-like sound. Such an intense pressure front can be created by
supersonic jet aircrafts flying at Mach 1. As
observed in the animation below, it is the source that is now leading the wavefront.

Jet pilots flying at Mach
1 report that there is a noticeable 'wall' or 'barrier' which must be
penetrated before achieving supersonic speeds. This is due to the
intense pressure front, and flying within this pressure front produces a
very turbulent and bouncy ride. The figure below shows a jet fighter at
the exact instant it goes supersonic. Notice the smaller shockwave
behind the pilot's cockpit.

(U. S. Navy photo by Ensign John Gay)
|